Scribe Post - February 23, 2010 - Madison

Hey y'all,
Today in class we learned about Arc Lengths and the Area of a Sector.

Starting with arc lengths Jojo told us that a unit circle has a radius of 1.

A unit circle looks like this:

The distance of an arc is one from one point to another on the circumference of a circle. And every degree measurement has a radian measurement. For example, 90 degrees = pi/2

Arc length is basically how many times degrees go into 360deg/pi.

We learned two equations on how to find arc length using both degree measurements and radian measurements.

For radians: (Where S is the arc length, alpha is the measurement in radians, 2pi is the total measure of the radian circle and 2pi r is the circumference)

For degrees: (Where S is the arc length, beta is the degrees in the subtended angle in the arc*, 360 is the total number of degrees in a circle, and 2pi r is the circumference)

*remember that subtended angles are angles that directly correspond with an arc. (we learned that earlier this year)

So if you plug in radians for the first equation and degrees for the second equation you should get the same answer. That's how you know you did it right!

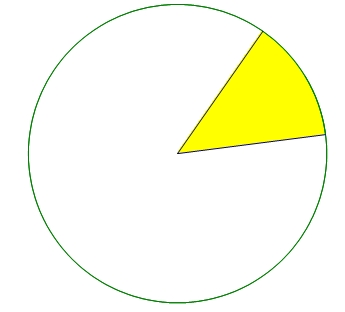
We also learned about finding the Area of a Sector

It's basically like finding the slice of pizza from the entire pie. So it looks like this:

To find the area of the sector we use two equations.

For Degrees: (Where A is the area, alpha is the subtended degree, 260 is the total number of degrees in a circle and pi r^2 is the formula for area)

For Radians: (Where A is the area, beta is the radian degree, 2pi is the total number of radians in a circle and pi r^2 is the area formula)

Again, if you plug in degrees for the first equation and radians for the second you should get the same answer.

Sorry this is so long. Hopefully it helped. If not helpful websites:

http://www.mathwords.com/r/radian.htm

http://www.mathsisfun.com/geometry/circle-sector-segment.html

Next scribe is Shake.

--Madison