Hey everyone,
Before I start, I must apologize for posting this so late, I only just got to a computer.
Today in class, we did more review on trig functions. Jojo worked through a few of the homework problems with us. We did not use calculators, but instead found the exact values of each problem we worked out. The method my class period used most was the unit circle method, where you use the unit circle to find the values of
,
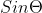
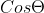
, and
.
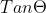
For example:
To solve this, you must first use the chant Jojo taught us, 30, 15, 15, 30, to find the location of the angle in the unit circle.
http://www.mathpeer.com/images/trig/unit_circle.gif That is a link to a picture of a unit circle. If you have one of these on hand, you can simply look at it and find 135 degrees, which is halfway between
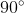
and
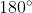
. The given angle is
.
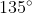
Jojo told us that an easier way to work with any angle would be to treat it as if it were in the first qudrant. So
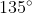
in the first quadrant becomes
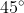
. To find
 "Sin (135^{\circ})")
, start by forming a right triangle with the radius used to form the angle and the horizontal axis. This will form a 45-45-90 triangle, which means that the two legs will equal 1 unit, and the hypotenuse, which is the radius, will equal
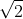
. Now,
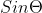
is a function, which is equal to
. So
%20=%20\frac{1}{\sqrt{2}} "Sin (135^{\circ}) = \frac{1}{\sqrt{2}}")
. You cannot leave
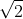
in the denominator, because it is a rational number, so multiply both the numerator and the denominator by
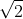
. This will leave you with
%20=%20(\frac{\sqrt{2}}{\sqrt{2}})%20(\frac{1}{\sqrt{2}}) "Sin (135^{\circ}) = (\frac{\sqrt{2}}{\sqrt{2}}) (\frac{1}{\sqrt{2}})")
, which multiplies out to be
%20=%20\frac{\sqrt{2}}{2} "Sin (135^{\circ}) = \frac{\sqrt{2}}{2}")
., if it is in the first quadrant. Now, a 135 degree angle will be in the second quadrant. Because a
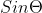
equation will only deal with y-coordinates, the answer will not become negative because the y-coordinates in the second quadrant wil lbe positive.
I do hope all of this made sense.
As a side note before I post: In case anyone has not posted this link,
http://www.codecogs.com/components/equationeditor/equationeditor.php will take you to an HTML equation editor, which is quite useful for posting on blogspot as at the top of the page (at least when i am posting) there is the option to edit HTML. Simply type the desired queation, and it wil ltranslate the equation into HTML code. Then cpoy and past this code into the desired place under "Edit HTML" part of the post, and the equation will appear in the text. This sounds confusing, but its simple once you get the hang of it. Hope this helps.
Marc
RSS Feed (xml)
Posts
